Learning Math/CS/Engineering Design with Robotics
Pythagorean Shell
|
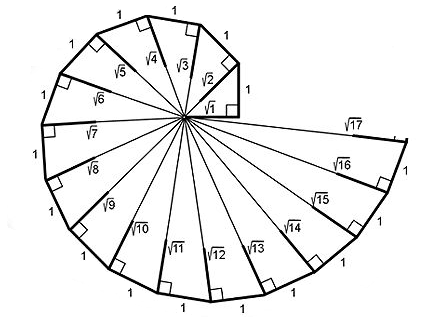
In this activity, you'll be recreating this spiral shell using Pythagorean Theorem.
|
| Grid Size: S M L | Simple View: | MinView: |
| Coord: x-axis y-axis | Grid Lines: x-axis y-axis | |||
| Grid: | 12x12 inches | 24x24 inches | 36x36 inches | |
| 72x72 inches | 96x96 inches | 192x192 inches | ||
| 1x1 inches | 2x2 inches | Fraction: | ||
| xy-Range: | ||||
|
|
||||
|
|
||||
| Quad: | 1 Quadrant | 4 Quadrants | 1&4 Quadrants | |
| Units: | US Customary | Metric | Ruler: | |
| Labels: |
|
|
|
|
Font
px
|
|
| Tics Lines: |
|
Width
px
|
| Hash Lines: |
|
Width
px
|
1. Linkbot
|
(
,
in
) in
|
|
degrees
|
|
Width
px
2. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
3. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
4. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
5. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
6. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
7. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
8. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
9. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
10. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
11. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
12. Linkbot
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
1. OmniBotA
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
2. OmniBotA
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
3. OmniBotA
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
4. OmniBotA
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
5. OmniBotA
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
6. OmniBotA
|
(
,
in
) in
|
|
|
degrees
|
|
Width
px
|
|
The outer perimeter of a Pythagorean spiral shell is drawn on the grid. Your job is to use the robots to finish the drawing by connect the origin to each dot on the shell's outline. The first example is done for you, driving robot 1 to the second dot at (3,3). Modify the green driveDistance() to drive robot 2 to the 3rd dot and the blue driveDistance() to drive robot 3 to the 4th dot. Finally add in more commands blocks to have robot 1 or 4 to complete the rest of the lines. Dots are numbered in counter-clockwise manner, starting at (3,0). The turning angle Θi between each dot (see initial prompt) are 45, 35.26, 30, 26.57, 24.10, 22.21, 20.71, 19.47, 18.44, 17.55, 16.78 degree counterclockwise respectively. |
|
Pre-Board Workspace
|
|||||||||||
Post-Board Workspace
|
|||||||||||